Optimizers
一、Optimizer
神经网络作为一个优化问题,优化函数的选择成为了训练过程的关键。但是对于现代的网络框架来说,反向传播封装成一个黑盒,造成我们只需要几行代码就可以完成整个反向传播的过程。这给初学者带来了极大的方便,但是对于想进一步深入理解神经网络的人来说,就造成了很大的困扰。本文就是想将反向传播中最重要的一环优化器剥离出来,希望能够对各位深入理解神经网络带来帮助。
梯度下降中参数更新的基本方法:
$$\theta = \theta - \eta \cdot \nabla J(\theta;x)$$
其中θ为网络参数,η为学习率。
1. In Tensorflow
Tensorflow支持目前所有常见的优化器,例如SGD、 Momentum、 Adagrad、 AdaDelta、 RMSProp, Adam。
再详细介绍各个优化器之前,首先看一下他们的基类Optimizer。
这些优化器包含一个minimize()方法,该方法用来优化目标函数,函数原型如下:
minimize(
loss,
global_step=None,
var_list=None,
gate_gradients=GATE_OP,
aggregation_method=None,
colocate_gradients_with_ops=False,
name=None,
grad_loss=None
)
第一个参数loss为不同人物定义的目标函数,第二个参数global_step用于更新全局的迭代次数,第三个参数var_list是graph中所有的可以训练的参数。
优化过程一般包括三个步骤:
-
Compute process. 计算
var_list中的参数梯度。 一般使用compute_gradients()。compute_gradients(loss, var_list),一般输入这两个参数,计算对应参数的梯度,返回值是(gradient, variable)对。 -
Pre process. 对梯度值进行一定的预处理,例如
clip等。有些时候可能会由于一些地方的梯度过大,造成在更新梯度的时候出现
NaN的情况,为了使训练尽可能的稳定,所以需要tf.clip_by_xxx() -
Apply process. 将不同的梯度值更新到对应的参数。一般使用
apply_gradients()。apply_gradients(grad_and_vars, global_step),使用第一步或者第二部处理之后的(grads, vars)进行更新,并且更新global_step。
正常情况下,Dr.Sure不会直接使用minimize(),因为它缺少步骤2中对梯度的一些精细操作。另外可以通过调整var_list中变量的数量、种类,达到精确控制某个变量更新规则的目的。同事通过将var划分到不同的list,也可以对不同的变量使用不同的learning rate或者不同的optimizer。
2. Challenge
- 学习率的选择,学习率是控制参数更新的一个最重要的参数之一,太小的学习率更新速度慢而且容易陷入局部最小,太大的学习率容易在学习过程中产生抖动。
- 如何调整学习率,一般来说我们会在训练的过程中动态调整学习率,也就是通过一个schedule,但是这个调整计划是我们预先设定好的,并不能根据不同的数据集动态去调整。
- 学习率被统一应用在了所有的参数上,即所有参数使用相同的学习率。但是这明显不是最优的选择,对于一些出现频率很小的参数,可能我们需要用更大的学习率,反之亦然。
二、Momentum、NAG
1. Momentum
Momentum是在原始的GradientDescent更新方法上的改进,其核心思想就是把动量的概念引入到参数更新的过程中。
动量一词来源于牛顿第一定律:任何物体都要保持匀速直线运动或静止状态,直到外力迫使它改变运动状态为止。“惯性”,即物体总是倾向于保持器原有的运动状态。对于参数更新也不例外,即本次更新会受到上次参数更新的梯度方向的影响。其计算公式如下:
其计算公式如下$$v_t=\gamma v_{t-1} + \eta\nabla _\theta J(\theta)$$
$$\theta=\theta-v_t$$
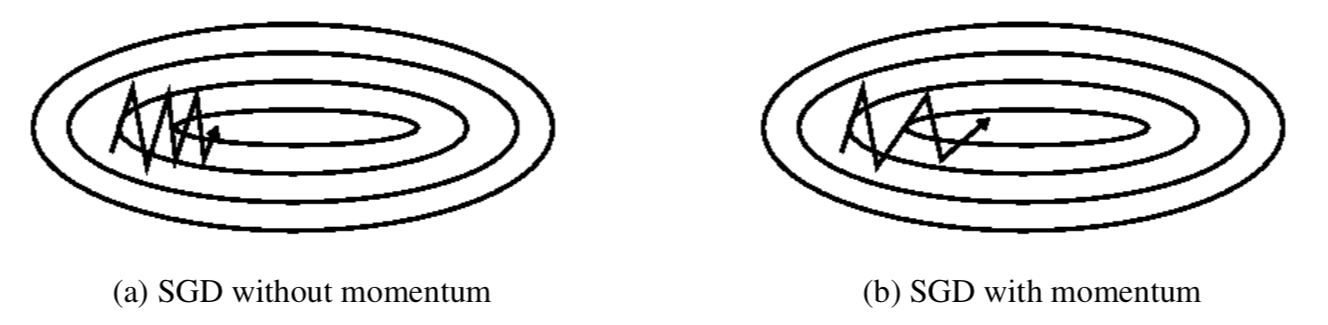
动量的引入就是为了加速参数更新的速度,同时为了平抑某次不一致的参数更新方向。如下图:
2. Nesterov accelerated gradient(NAG)
从上面的vt计算的公式中可以看到,在计算当前步骤的梯度时仍然使用的是当前的参数,优化函数本身已经通过引入动量来加速整个参数更新的过程了,参数也可以“Look forward”?
Nesterov accelerated gradient(NAG)的优化方法就是因此而来。其vt的计算公式如下:
的计算公式如下$$v_t=\gamma v_{t-1} + \eta\nabla _\theta J(\theta - \gamma v_{t-1}) $$
3. Momentum In Tensorflow
__init__(
learning_rate, # 学习率,根据任务自行设定。
momentum, # 动量,一般设置成0.9或者其它更小的值。
use_locking=False,
name='Momentum',
use_nesterov=False # 是不是使用Nesterov方法对其进行加速。
)
三、Adagrad、Adadelta、RMSProp
虽然Momentum以及NAG加速了参数训练的过程,但是它仍然存在一个弊端那就是所有的参数均使用一个相同的学习率。
1. Adagrad
Adagrad根据不同的参数调整学习率。对于经常出现的梯度的参数,采用较小的学习率,不经常出现的梯度的参数,采用较大的学习率。因此该更新方法特别适合那些稀疏数据。
其更新公式如下:
$$\theta_{t+1, i}=\theta_{t,i}- \frac{\eta}{\sqrt{G_{t,i}+\epsilon }}\odot g_{t,i}$$
Gt计算的是当前时刻,每一个参数梯度的平方。从公示中可以看出,在t时刻,每个参数都有一个Gt对应于其历史的所有梯度平方之和,这就使得每一个参数在任意时刻的学习率并不是完全一样,而这个学习率完全依赖于其历史的参数。
这样的更新方法当然可以使得“少见”的参数梯度比较大,而“常见”的参数梯度比较小。但是这个参数更新的方法会造成一种极端的情况:随着迭代次数的增加,G的积累值会越来越大,最后会使得学习率η趋向于0,造成无论怎样更新,参数都不会发生变化。
2. Adadelta
Adadelta为了解决Adagrad训练过程中学习率调整为零的情况。其具体做法就是将原来的G由“所有”历史梯度的平方和修改成移动平方和。
类似于动量的求解方法,梯度平方和矩阵的求解方法如下:
$$E[g^2]_t=\gamma E[g^2]_{t-1}+(1-\gamma)g_t^2=RMS[g]_t$$
文中作者发现,learning_rate也可以使用参数自身的移动平方和进行表示。
$$E[\Delta \theta^2]_t=\gamma E[\Delta \theta^2]_{t-1}+(1-\gamma)\Delta \theta^2=RMS[\Delta \theta]_t$$
所以最后的更新公式为:
$$\theta_{t+1}=\theta_{t}-\frac{RMS[\Delta \theta]_{t-1}}{RMS[g]_t}g_t$$
3. RMSProp
RMSProp是Adadelta的一种特殊情况:
$$E[g^2]_t=0.9E[g^2]_{t-1}+0.1g_t^2=RMS[g]_t$$
$$\theta_{t+1}=\theta_{t}-\frac{\eta}{RMS[g]_t}g_t$$
4. Adagrad、 AdaDelta、 RMSProp in Tensorflow
__init__( ## Adagrad
learning_rate,
initial_accumulator_value=0.1,
use_locking=False,
name='Adagrad'
)
_init__( ## Adadelta
learning_rate=0.001,
rho=0.95,
epsilon=1e-08,
use_locking=False,
name='Adadelta'
)
__init__( ## RMSProp
learning_rate,
decay=0.9, # γ,Discounting factor for the history/coming gradient
momentum=0.0,
epsilon=1e-10,
use_locking=False,
centered=False, # If True, gradients are normalized by the estimated variance of the gradient; if False, by the uncentered second moment.
name='RMSProp'
)
四、Adam
Adam的核心思想结合了Adadelta的移动平均以及Momentu的经验衰减。
其动量的两个分量分别表示为:
$$m_t=\beta_1 m_{t-1} +(1-\beta_1)g_t$$
$$v_t=\beta_2 v_{t-1} +(1-\beta_2)g_t^2$$
mt和vt在初始化的过程中被统一设置成0,这就造成了优化的初始阶段,是的他们的值非常小,尤其是当β趋近于1的过程中。
为了解决这个问题,作者使用下面对mt和vt进行估计:
$$\hat {m_t}=\frac{m_t}{1-\beta_1^t}$$
$$\hat {v_t}=\frac{v_t}{1-\beta_2^t}$$
因此最终的形式变成:
$$\theta_{t+1}=\theta_t-\frac{\eta}{\sqrt{\hat{v_t}}+\epsilon }\hat{m_t}$$
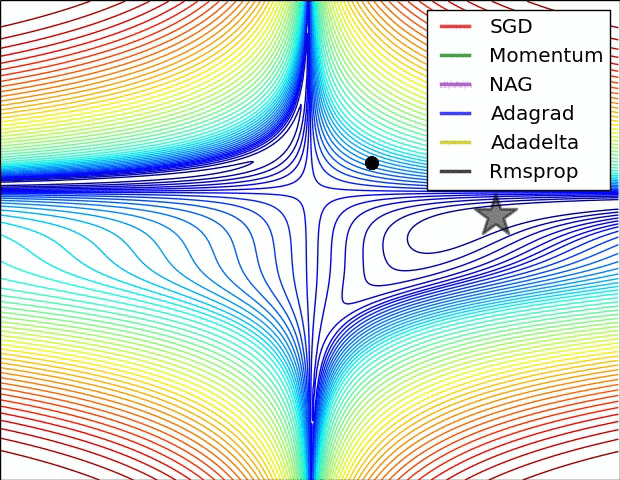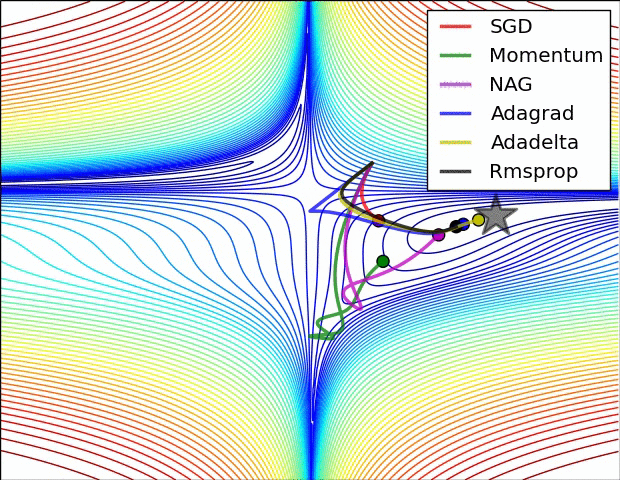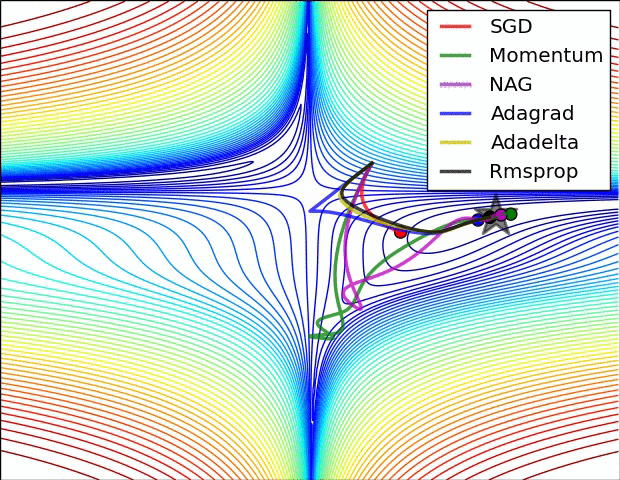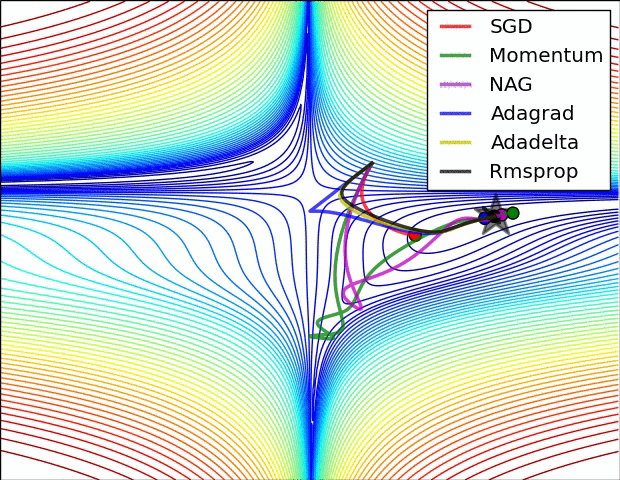
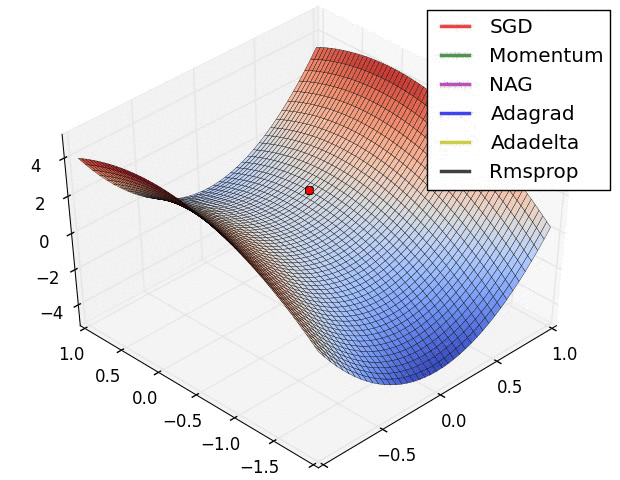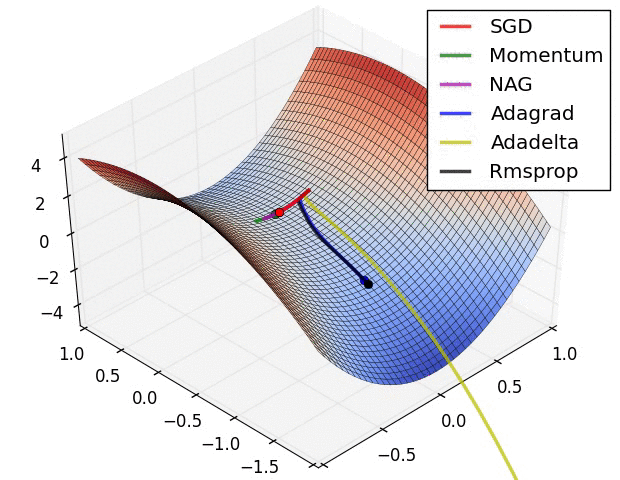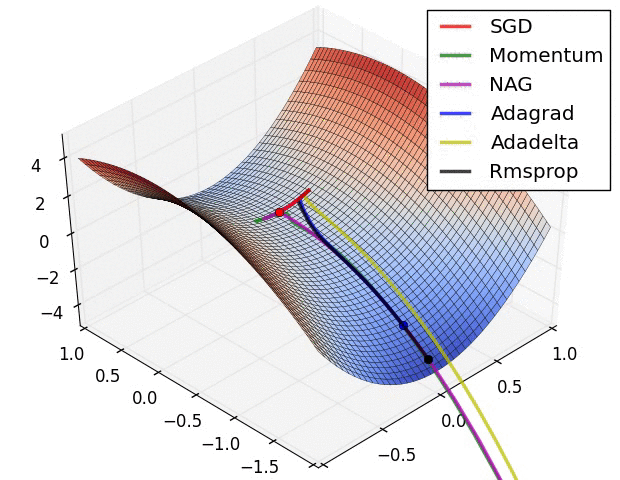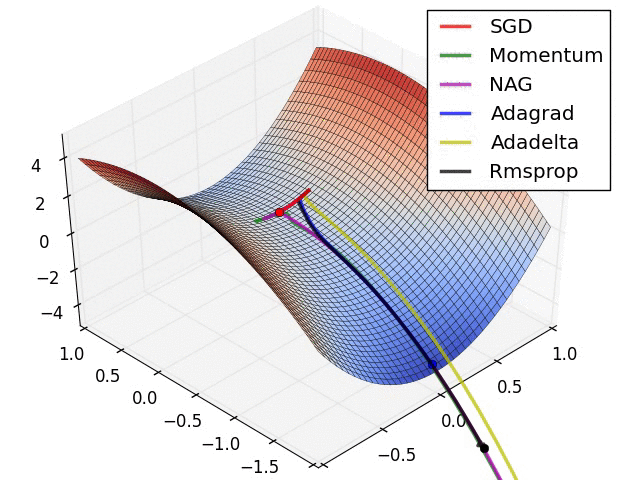
五、Visualization